具体介绍了双锥流量计的基本原理，提出了一种基于LS-SVM 的双锥流量计气体流量测量方法。在介绍了双锥流量计的基本结构的基础上，详细阐述双锥流量计流出系数的实验标定方法及可膨胀系数计算公式的确定算法，软测量中辅助变量的选择、数据预处理、测量模型的建立及训练测试等内容。并归纳阐述了支持向量机的基本原理，实现最小二乘支持向量机的过程和算法。最终建立了双锥流量计气体质量流量测量的LS-SVM 数学模型。结果表明：采用基于LS-SVM 的双锥流量计进行流量计量，可以确保测量结果在工业计量要求范围内具有较高的测量准确度。

引 言

气体流量测量是计量测试的一类重要检测技术，在流量计量行业占有极其重要的地位，测量的在线分析结果对于准确有效地实施过程控制具有非常重要的意义。通常采用的传统测试方法，如非在线分析、直接参数控制、电子检测与显示仪表等都存在一定程度上的不足[1]。然而，软测量技术的应用为解决此问题提供了新方法。支持向量机（SVM）是一种新的基于数据的机器学习方法，它是随着统计学习理论的发展和成熟而得付储实践的应用方法。SVM 能够尽量提高学习机的推广能力，即使由有限数集得到的判别函数对独立的测试集仍能够得到较小的误差。最小二乘支持向量机是SVM 的扩展。在设计参数确定的情况下，将其应用于双锥流量计测量气体流量能确保一定的测量精度[2]。因此，实验研究提出一种基于LS-SVM 的双锥流量计气体流量测量仿真研究方法。

1.双锥流量计的测量原理

差压式流量计的基本原理是依据测得节流件前后不同取压点的压力差，进而按照相关公式计算出所测量的流体流量。

 双锥流量计简化结构如图1 所示。

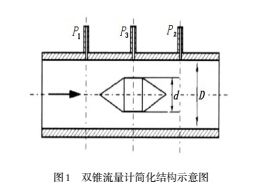
根据伯努利方程和流体计算的连续性方程，得出双锥式差压流量计的流量qv 与差压Dp 间的关系满足下列公式：

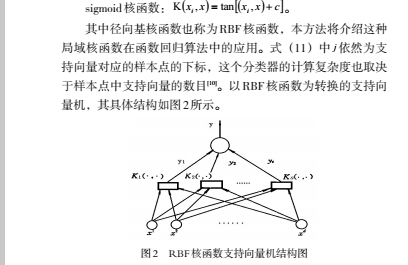
3.最小二乘支持向量机在函数逼近中的应用

SVM 的训练是一个二次规划问题，有一定的约束条件，其约束量等于样本的大小，这个特征点引起训练耗时较长，尤其是当训练样本容量较大时，总耗时过长往往会导致测量结果不佳。

为减少支持向量机的训练时间，改变标准支持向量机的约束条件和损失函数，导出了一种新的支持向量机，最小二乘支持向量机(Least Squares Support Vector Machine，简称LS-SVM)。对于LS-SVM 的训练结果求取，只需解一组以训练样本为系数的线性方程。这使SVM 模型得到了极大的简化，在很大程度上提高了SVM 模型的训练效率。最小二乘支持向量机作为支持向量机的一个分支，由于其计算量小、计算速度高等特点，目前广泛应用于各种分类问题和函数逼近问题中。

 最小二乘支持向量机应用误差的2-范数代替支持向量机中的松弛因子的和，即把下列式作为损失函数：

4.LS-SVM 模型的建立及实验

4.1 模型的训练及验证

通过分析和研究，建立气体流量测量的LS-SVM 模型。应用数学计算方法、查表法和迭代算法等可获得被测气体的流量。

由公式(2)、(3)可知，dn、Dn ® d、D ；由公式(8)可知， p1、t ® r ；

由公式(4)、(7)可知，d、D、Dp、p1 ® b、e ；由公式(1)、(5)、（6）可知，e、A0、Dp、b、r 通过多次迭

代计算® C、qm 。

实验中，采用的训练样本集为静压、温度、压力差为输入量，以质量流量为输出量，通过多次训练得到一个LS-SVM 模型。压力 p(kPa ) 、温度t(°C ) 、差压Dp(Pa ) 的取值如下：

其中t 、 p 、Dp 均采用特定的向量模式。应用不同的温度、静压、压力差的多样组合则可以得到一定容量的样本。各选取其中90 组分别作为测量的样本训练值和预测值。通过仿真计算，得到的流量测量实验结果如图3 所示。

仿真实验中一组的数据作为训练样本集，得到LS-SVM 的预测模型。并用另一组数据作为测试样本对获得的模型进行检验。由图3 可知 ，得到的预测结果和测试结果相差很小。

4.2实验的误差分析

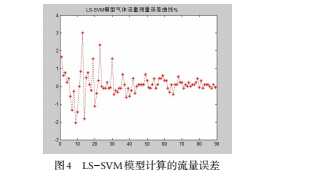
仿真实验通过对LS-SVM 的预测值和检验值进行对比分析，得到的误差如图4 所示。

由图4 可知，LS-SVM 模型的输出值与检验值的最大相对误差逐渐收敛且小于2%。仿真实验结果证明，此方法计算流

量结果的稳定性高且满足工艺要求的测量精度。

5.结 论

本文针对双锥流量计气体流量测量的实际问题，采用了工业领域中常用的软测量建模手段，提出了LS-SVM 相结合的软测量建模方法。应用研究结果表明，模型对双锥的流量特性具有很好的逼近能力和泛化能力，可以保证全量程范围内较高的准确度，具有一定的工程应用价值。该方法具有学习能力强、小样本计算和运算时间短等优点，可以在各种流量计量领域中具有广泛的应用前景。