由于强噪声背景下的多普勒超声波回波信号属于微弱信号，传统谱分析方法对微小多普勒偏移量的测量误差较大，使得现有的超声多普勒流量计在应用范围和测量精度上受到限制，因此提出采用 Zoom FFT 结合卡尔曼滤波来提高多普勒流量计的测量精度。文中首先采用 Zoom FFT 来提高多普勒回波信号的频率分辨率，然后通过卡尔曼滤波器递推跟踪频率偏移值，最后在 Matlab 环境下实现了 Zoom FFT 算法和卡尔曼滤波算法。现场测试结果表明: 采用 Zoom FFT 结合卡尔曼滤波可以提高流量测量精度。

0.引言

采用多普勒效应制造的超声波流量计因其非接触、安装方便，在很多行业都得到了广泛的应用，被认为是非接触式测量的理想仪表。根据多普勒频差法的测量原理，流速的分辨率直接影响了流量的分辨率，也直接影响了流量的测量精度。由于在测量过程中流速不稳定、管道的偶尔振动都会导致利用超声波多普勒法测量时无法得到稳定的频率偏移量 。目前常用的获取频率偏移量的方法是采用传统的傅里叶变换，采用该方法提高频率分辨率只能增加采样点数，但是 DSP 的内存是有限的，数据量越大必然会影响 DSP 的运行速度，本文采用 Zoom FFT 来提高流速的分辨率，Zoom FFT 适用于对宽的频率分析范围、高频率分辨率和较少采样点数的场合 。该方法可以在不增加点数的情况下 提高频率分辨率。在利用多普勒频差法计算流量时需要确定频差，确定频差就必须进行峰值搜索，搜索的最简单方法是采用多点平均值法或者采用平滑滤波器，但是这两种方法由于没有考虑连续几个点之间的递推性，所以流量测量误差较大。卡尔曼滤波是一种时域的滤波方法，适合于递推求解。数据可以逐一实时处理，即将每个采样时刻获得的频率偏移量的峰值数据立即处理，并与基于该时刻以前的状态估计值一起，由递推方程随时给出新的状态估计，所以本文采用卡尔曼滤波器跟踪下一个时刻的流速值。

1.多普勒超声流量测量模型

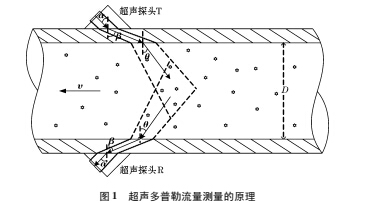
图1 为连续波超声多普勒管道流量测量原理图。多普勒超声流量测量的原理是基于物理学中声波的多普勒效应。当声源与观测者之间存在相对运动时，观测者所感受到的声波的频率与声源所发出的频率存在一定的频率差，即声波的频率因相对运动而发生了改变，并且这个频率的变化量正比于两者之间的相对运动速度，这就是多普勒效应。

在已知管道直径 D 的情况下，可求得管道内的瞬时流量Q:

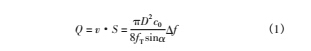
式中: c0  为声楔中的声速; α 为声楔的角度; fT 为发射频率。

当探头选定后，c0 、α 及 fT 就已固定，所以只要测出多普勒频移量 f 就可计算出管道内的流体流动速度 v． 从式( 1) 可以看出要提高流量测量的准确性，必须提高频差的频率分辨率，本文采用 Zoom FFT 通过对频率的细化达到提高频率分辨率的目的; 同时因为流体中的声速 υ 及声波传播方向容易受到流体环境变化的影响，在测量过程中如果瞬时流量 Q 保持不变，但是频差 f 的值总是随着时间在变化，因此需要一种具有递推能力的信号处理算法来跟踪频差 f 的峰值，卡尔曼滤波算法正好具有递推的功能 因此本文选择卡尔曼滤波算法 。

2.基于复调制细化 Zoom FFT 提高频率差的分辨率

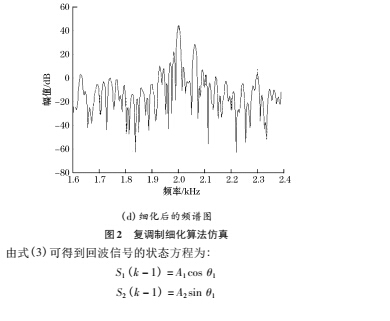
对于在同一流速下的多普勒频移信号，假设采样点数为8 192，细化倍数为 8，滤波器的阶数 M = 32，根据 Zoom FFT 的特点，只需做 1 024 点的 FFT，分辨率即可达到 1． 526 Hz。图 2 为仿真结果。

3.基于卡尔曼滤波原理的峰值跟踪法

由于多普勒频移信号的峰值容易受流速、外部干扰等的影响，因此具有明显的随机性。卡尔曼滤波器是一套由数字计算机实现的递推算法，每个递推周期中包含对被估计量的时间更新和测量更新两个过程。时间更新由上一步的测量更新结果和设计卡尔曼滤波器时的先验信息确定，测量更新则在时间更新的基础上根据实时获得的量测值确定。因此，测量量可看作卡尔曼滤波器的输入，估计值可看作输出。输入和输出之间由时间更新和测量更新算法联系。

3． 1 卡尔曼模型的状态方程

卡尔曼模型的状态方程为

S( k) = A( k) S( k － 1) + W( k － 1) ( 2) 式中: A( k) 为系统中 k － 1 时刻的状态到 k 状态之间的转移;

W( k － 1) 为系统噪声。

该公式表示 k 时刻的状态 S( k) 可以用其前一个时刻的状态函数 S( k － 1) 来表示。

观测方程为

X( k) = C( k) S( k) + V( k)             （3）

式中: V( k) 为观测噪声; C ( k) 为测量系统的参数，设定其与V( k) 为不相关且成正态分布的白噪声。

3． 2 基于卡尔曼滤波的回波测量模型

多普勒效应认为当发射换能器和接收换能器之间有相对运动的时候，接收换能器接收的声频率会发生改变，这个相对于声源频率的变化就是多普勒频移，其大小是正比于发射换能器与接收换能器之间的相对运动。多普勒流量计接收的回波信号由 2 部分组成: 一部分是由流体中的粒子或气泡等产生的反射回波; 另一部分是由换能器内部发射晶片直接耦合到接收晶片的直耦信号。它们在接收换能器上迭加形成，通过放大检波，获得的差频信号即为多普勒信号 。在测量过程中超声波换能器发射的信号为

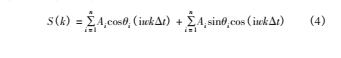
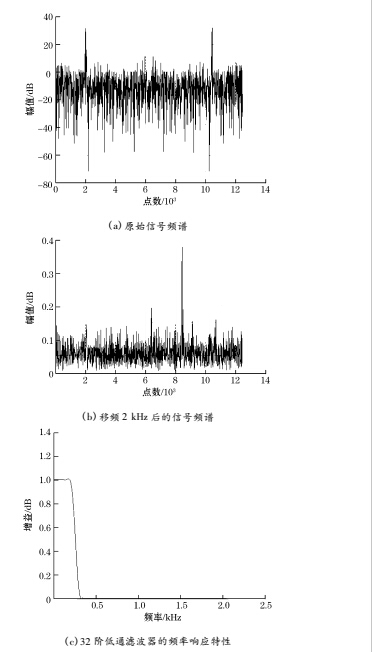
3． 3 仿真分析

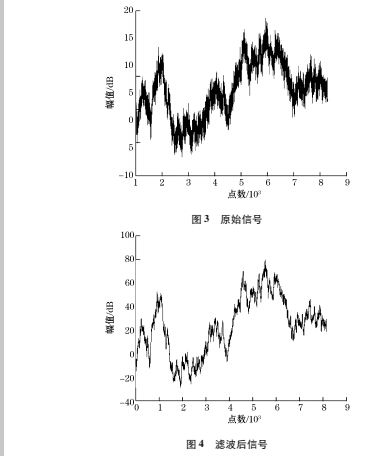
为验证卡尔曼滤波算法对超声波多普勒频率偏移信号的峰值跟踪功能，在 CCS 环境下，利用 MATLAB 编写算法。频移信号的中心频率为 2 kHz，采样频率为 12． 5 kHz，如图 3 和 4 所示。从图 4 可以看出，经过滤波后，信号中的噪声幅值明显比图 3 的原始信号小了。利用图 4 处理后的超声波多普勒频率偏移信号，根据式( 3) ～ 式( 9) 可以求出流量的最优估计值

4.试验验证和评估

在室内的油气井管道试验平台上，通过调整变频器的频率来模拟不同流速下的管道流量，混合流体为水和滑石粉，以质量流量计作为标定仪器。试验结果如表 1 所示。

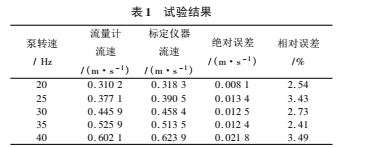
由该组试验数据可知，当变频器的频率分别为 20 Hz、25 Hz、30 Hz、35 Hz、40 Hz 时，采用本文所设计的信号处理方法后，超声波流量计的相对误差大概在 3． 5% 以内，流量测量结果满足工业现场的使用要求。

5.结论

为了提高多普勒流量计在流量测量时的精度，提出了 ZoomFFT 结合卡尔曼滤波的信号处理算法。文中首先通过 Zoom FFT来提高多普勒回波信号的频率分辨率，然后通过卡尔曼滤波根据估计误差对卡尔曼滤波状态进行估计，并调整卡尔曼滤波模型中的参数，实现对频率偏移量的跟踪，以得到较为准确的频率偏移量的估计值。试验结果表明: 所提出的信号处理方法具有提高多普勒法的频偏分辨率以及峰值跟踪的能力，实时性好、精确度高，具有很高的应用价值，能够满足现场的使用要求。